Toto je jedna z tých úžasne hlúpych otázok, ktoré na prvý pohľad nedávajú zmysel, ale keď sa nad nimy človek zamyslí, tak sa toho kopec dozvie. Takže čo táto otázka vôbec znamená? Priemernú hmotnosť predsa vždy rátame rovnako: vezmem všetky veci z danej kategórie, zrátam dokopy všetky ich hmotnosti a vydelím to ich počtom. Priemerný Američan tak váži \(80 \mathrm{ kg}\) a priemerný ananás \(2 \mathrm{ kg}\). Priemerná hmotnosť všetkých Američanov a ananásov dokopy zas vyjde okolo \(3,5 \mathrm{ kg}\) (ananásov je skrátka oveľa viac ako Američanov). No dobre, ale nás nezaujímajú nejaké takéto podmnožiny, my chceme priemernú hmotnosť VŠETKÉHO ! Galaxií, planét, tučniakov, atómov, kvarkov! Koľko to tak asi bude?

Hneď tu na začiatku narážame na problém. Ak zarátame do priemerovania napríklad človeka, možno by sme už nemali zahrnúť bunky z ktorých sa skladá, pretože hmotnosť každej z nich sme už zahrnuli. Takto definovaná otázka by nám ale veľa nepovedala. Mala by totiž triviálnu odpoveď, že všetko je súčasťou vesmíru, a tak teda existuje len jediná vec - vesmír. Miesto toho si problém radšej definujme takto: predstavte si, že sa hráte na boha [1] to predsa vedci podľa všetkých filmov radi robia, občas siahnete do vesmíru a vytiahnete odtiaľ nejakú vec. Môže to byť čokoľvek čo by niekto niekedy označil ako samostatnú vec, bez ohľadu na to, či je to súčasť niečoho väčšieho alebo nie. Odvážite ju, zapíšete si jej hmotnosť a vrátite ju naspäť. No a nás zaujíma, aká bude priemerná hmotnosť takto vyťahovaných vecí. Čo je ešte “vec” je samozrejme stále subjektívne, ale s trochou šťastia to výsledok príliš neovplyvní, keďže nám aj tak ide len o odhad. Poďme teda na to. Ale počkať! Ešte pred tým si tipnite koľko to vyjde. No vážne, nie že budete pokračovať bez hádania! Už máte? Tak pokračujeme.

Čo všetko by sme mohli považovať za veci? Najväčšia vec je vesmír (pozorovateľný). Váži \(m_{max}=10^{54} \mathrm{ kg}\) a je len jeden. Potom, keď trochu zazoomujeme, prejdeme na nižšiu škálu a zistíme že sa skladá napr. z kôp galaxií (Je to vec, alebo nie? To si zatiaľ necháme na neskôr, rovnako ako tmavú hmotu/ energiu). Potom sú galaxie, potom hviezdy, …, potom sú molekuly, potom atómy a potom elementárne častice. Skončíme napr. pri kvarkoch, tie váža \(m_{min}=10^{-30} \mathrm{ kg}\). Na základe tohoto si urobme jednoduchý model vesmíru: predpokladajme, že na každej hmotnostnej škále sa vesmír skladá z rovnakých vecí. Z tých sa zas každá skladá z \(N\) vecí na nižšej škále, ktoré sú teda N-krát ľahšie, atď. až po najmenšie častice, ako na obrázku 1. \(N\) budeme volať škálovací faktor. Keby napr. \(N\) bolo 2, tak by sa vesmír skladal z dvoch polvesmírov, tie každý z dvoch štvrťvesmírov, atď. až po dvojkvarky a o jednu škálu nižšie kvarky. Vidno že \(N=2\) nedáva dobrý zmysel, takže to asi bude nejaké väčšie číslo, ale to si zatiaľ odložíme.

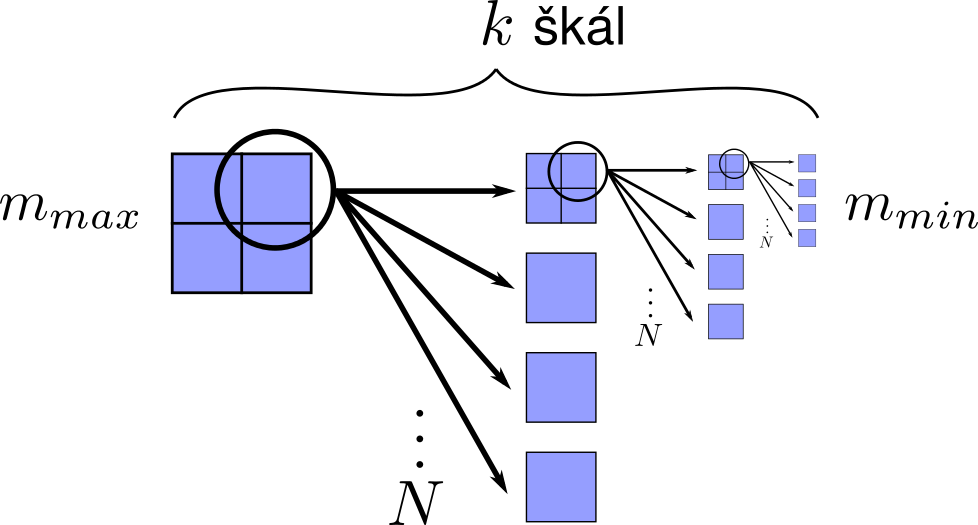
Obr. 1: Náš model vesmíru: každá vec sa skladá z \(N\) menších vecí, pričom dokopy je takto vesmír rozdelený na \(k\) škál. Na \(i\)-tej škále teda existuje dokopy \(N^{i-1}\) objektov.

S týmto predpokladom je už ľahké napísať vzorec pre priemernú hmotnosť. Rovno z definície (spočítaj hmotnosti všetkých vecí a vydeľ to ich počtom):

\[\begin{equation}\begin{split}\widetilde{m} &= \frac{m_{max}+\frac{m_{max}}{N}N+\frac{m_{max}}{N^2}N^2+...+\frac{m_{max}}{N^{k-1}}N^{k-1}}{1+N+N^2+\dots+N^{k-1}} = \\ \\ &= \frac{m_{max}\cdot k}{1+N+N^2+\dots+N^{k-1}} \end{split}\end{equation}\]

kde \(k\) je počet škál na ktoré vesmír delíme, tzn. \(k=1+\log_N{\frac{m_{max}}{m_{min}}}\). Po troche algebry [2] súčet konečného geometrického radu \(1+N+N^2 \dots N^{k-1}=\frac{N^k-1}{N-1}\) a fakt, že \(N^{k-1}=\frac{m_{max}}{m_{min}}\) a pár zanedbaniach [3] \(N^{k}-1 \approx N^{k} a \frac{N-1}{N} \approx 1\), dostaneme tento vzťah v nádhernej forme:

\[\begin{equation}\widetilde{m} \approx k \cdot m_{min}\end{equation}\]

To je prekvapivo jednoduchý výsledok na tak veľký problém. Zistili sme, že priemerná hmotnosť všetkého je jednoducho súčin dvoch premenných: počtu škál na ktoré rozdelíme vesmír a hmotnosti najmenších častíc vo vesmíre. Čo je ešte lepšie, je to vždy neuveriteľne malé číslo (\(m_{min}\) je predsa hmotnosť najľahších vecí vo vesmíre). Dôvod prečo je to tak je prostý: tých malých častíc je skrátka priveľa a dokopy vážia skoro toľko čo celý vesmír. Ak to chcete vidieť matematicky, tak si všimnite menovateľ vo vzťahu (1). To je obrovské číslo ktoré zaručene prebije hocičo v čitateli. Ach, zas ten exponenciálny rast…

V akom rozpätí môže vôbec priemerná hmotnosť všetkého byť? To závisí len od škálovacieho faktoru \(N\). Najvyššie možné \(N\) je \(N=10^{84}\), čiže také, pre ktoré má vesmír len dva typy objektov: celý vesmír a potom kvarky, nič medzitým. V takom prípade \(k=2\) a teda priemerná hmotnosť celého vesmíru bude rádu jeho najmenších častíc. Druhý extrém je veľmi malý škálovací faktor. Asi najmenší rozumný je \(N=2\) (každá vec sa skladá z dvoch menších vecí). Aj tak ale bude počet škál len úbohých \(k=280\) a priemerná hmotnosť všetkého sa tak nad hmotnosť elementárnych častíc zdvihne len o dva rády.

No dobre, poviete si, ale predpoklady z ktorých sme vychádzali neboli celkom kóšér. Vesmír nie je žiadny dokonalý fraktál, v ktorom sú na každej škále všetky veci rovnaké a dokopy tvoria celý vesmír. V skutočnosti sa niektoré veci skladajú z objektov až o niekoľko škál nižšie a škály sa teda “preskakujú”. Napríklad také hviezdy sa skladajú priamo z atomárnych jadier a elektrónov a tak preskočíme zo škály hviezd (Slnko váži \(10^{30} \mathrm{ kg}\)) rovno na škálu elementárnych častíc (\(10^{-27} \mathrm{ kg}\) a menej), čím sme sa úplne vyhli škále ľudských rozmerov! Takisto, škálovací parameter sa bude meniť v závislosti od toho, na akej škále sme. A čo ešte taká temná hmota a temná energia? A čo väzbová energia, ktorá prispieva k hmotnosti atómových jadier (a kadečoho ďalšieho) skrz \(E=mc^2\)? Kam zarátať tú?

Keďže toto nie je vedecký článok ale len odpoveď na hlúpu (ale dobrú!) otázku, tieto problémy nenápadne opomeniem. Dám vám ale pár argumentov prečo podľa mňa výslednú odpoveď príliš neovplyvnia. Je dôležité uvedomiť si, že keď sa bavíme o priemernej hmotnosti, hlavné slovo nemá to čo váži najviac, ale to čoho je najväčší počet. Vezmime si napr. takú temnú energiu. Tvorí síce dve tretiny hmotnosti vesmíru, ale je to len jeden objekt [4] Je možné že sa raz bude na školách učiť, že sa z niečoho skladá, ale zatiaľ je väčšinou braná ako jedna vec. . Na druhej strane elementárnych častíc je \(10^{84}\) a dokopy vážia rádovo takmer rovnako ako temná energia, takže úplne ovládnu to aká bude hodnota priemernej hmotnosti. Kto neverí, dosaďte si do vzorca. Na to aby nejaká vec ovplyvnila výsledok výrazne, muselo by jej byť neuveriteľne veľa, a na to zas musí mať nízku hmotnosť, takže by s priemernou hmotnosťou všetkého aj tak veľmi nepohla. Ďalší problém je preskakovanie škál. Vzorec (1) by sa dal upraviť tak, aby ho vzal do úvahy, a to takto:

\[\begin{equation}\begin{split}\widetilde{m}&=\frac{m_{max}+f_1 m_{max}+f_2 m_{max}+ \dots +f_{k-1}m_{max}}{1+N+N^2+\dots+N^{k-1}}= \\ \\ &=\frac{\widetilde{f}m_{max}\cdot k}{1+N+N^2+\dots+N^{k-1}}\end{split}\end{equation}\]

kde sme zaviedli \(f_i\), čo je pomer celkovej hmotnosti vecí na i-tej škále k celkovej hmotnosti vesmíru. To sa dá ale zhrnúť zavedením priemernej hodnoty tohoto parametra \(\widetilde{f}\), čo je číslo určite menšie ako 1, a zbytok vzorca je potom taký istý. Takže preskakovanie škál môže výslednú priemernú hmotnosť len znížiť.

Dospeli sme teda k serióznej odpovedi: priemerná hmotnosť všetkého je niekde na úrovni hmotnosti elementárnych častíc (plus mínus dva rády). Čo si z toho odniesť? Niečo o exponenciálnom raste: je totiž príčinou toho, prečo je elementárnych častíc tak strašne, strašne,…, strašne veľa. Tak veľa, že všetkého ostatného je oproti nim zanedbateľne málo. A ešte si odneste aj niečo o priemeroch: zmazávajú stopy po všetkých výnimkách, pokiaľ nie sú teda fakt veľké. A čo sa týka vecí vo vesmíre, čokoľvek ťažšie ako elementárna častica JE výnimka.