\(\newcommand{\refr}[1]{(\ref{#1})} \newcommand{\tvect}[2]{ \begin{pmatrix} #1 \\ #2 \end{pmatrix} } \newcommand{\bra}[1]{ \langle #1 \rvert } \newcommand{\ket}[1]{ \lvert #1 \rangle } \newcommand{\braket}[2]{ \langle #1 \lvert #2 \rangle }\)Ha, dostal som vás! Tento článok je v skutočnosti o kvantovej mechanike a Dirac, tvorca bra-ket notácie, sa teraz smeje vo svojom hrobe [1] Aj keď je pravda, že táto interpretácia názvu bra v Diracovej dobe ešte pravdepodobne nebola možná. Termín bra pre podprsenku bol prvý krát použitý v Holandsku len 15 rokov pred zavedením bra-ket notácie a šíril sa len pomaly. . Konkrétne sa tu dozviete niečo o bra a ket (to sú tie zobáčikové zátvorky \(\ket{}\)a \(\bra{}\) ) a hlavne o tom, ako pomocou nich zapisovať operátory v kvantovej mechanike. Tento článok je určený pre všetkých, ktorí si už s kvantovou mechanikou čo to odžili (študenti na Matfyze, ktorí sa práve boria s Kvantovkou I, sa sem rátajú), ale mätú ich tie divné zátvorky a čo s nimi občas ľudia stvárajú. Ak do tejto kategórie spadáte, čítajte ďalej.

Bra-ket notácia je skvelá v tom, že zachováva abstraktný charakter pojmov, ktoré ňou popisujeme, a nelipne na ich konkrétnej reprezentácií. Nezáleží na tom, či stavy popisovaného systému reprezentujeme ako usporiadané n-tice čísel, kvadraticky integrovateľné funkcie (a.k.a. vlnové funkcie), alebo nejakým iným obskúrnym spôsobom. Dôležité je len to, že sú to vektory. Funguje to takto:

Ket \(\ket{.}\)

Ket sú stavy systému. Sú to teda vektory zo stavového priestoru [2]Ak je fakt, že stavy sú vektory, pre vás novinka, tento článok vám nič nedá. Skúste najprv zelenú knižku alebo inú učebnicu a potom sa vráťte. a môžeme ich sčitovať a násobiť komplexnými číslami. Pojmy stav a vektor tu budem teda voľne zamieňať. Čokoľvek vnútri zátvorky pritom slúži len ako nálepka, charakterizujúca konkrétny vektor. Napríklad \(\ket{1}\) je stav ktorý sme označili číslom \(1\), \(\ket{init}\) môže byť označenie začiatočného stavu. Často sa stretnete aj s takýmto zápisom: \(\ket{x}\). Tu si treba uvedomiť, že \(x\) nie je premenná, ale nejaká konkrétna hodnota \(x\).

Bra \(\bra{.}\)

Bra sú lineárne funkcionály na stavovom priestore. Funkcionál je mlynček. Na vstupe vezme stav a do klobások natlačí číslo.

\[\begin{equation} \bra{\phi}\ket{\psi}=\braket{\phi}{\psi}=c \;\;\;\; c \in \mathbb{C} \end{equation}\]

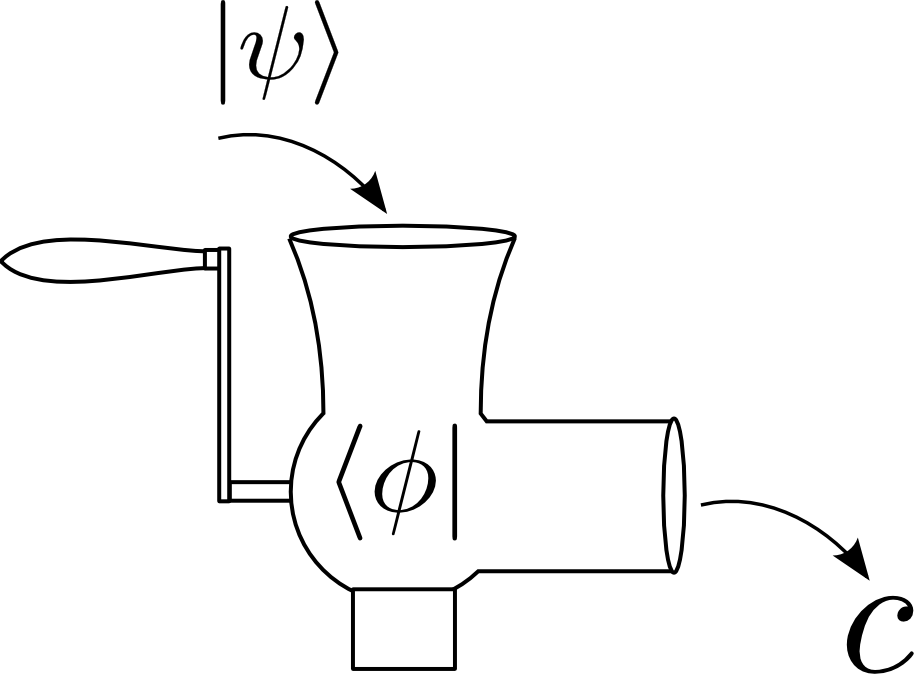
Tieto funkcionály sú definované tak, aby boli konzistentné so skalárnym súčinom, ktorý musí byť na stavovom priestore definovaný. Takže skalárny súčin vektorov (stavov) \(\psi\) a \(\phi\) vieme zapísať ako:

\[\begin{equation} {\psi} \cdot {\phi}=\braket{\psi}{\phi} \end{equation}\]

Dobrá správa je, že takto definované funkcionály opäť tvoria vektorový priestor, tzv. duálny k pôvodnému stavovému priestoru. Takže aj bra môžeme navzájom sčitovať a násobiť komplexnými číslami. Pre väčšinu účelov je ale dôležité len pamätať si, že \(\braket{ . }{ . }\) je skalárny súčin dvoch vektorov.

Ešte pár pravidiel, ako manipulovať s bra vektormi. Bra pôsobí vždy doprava, na stav ktorý je bezprostredne za ním. Takže tento výraz

\[\begin{equation} \bra{\psi} \ket{\phi}\ket{\xi}=\braket{\psi }{ \phi} \ket{\xi} \end{equation}\]

znamená skalárny súčin vektorov \(\psi\) a \(\phi\) (čo je číslo), ktorým je prenásobený vektor \(\xi\). Ak bra pôsobí na zložený výraz, jednoducho ho roznásobí (čo vyplýva priamo z toho, že skalárny súčin je bilineárny):

\[\begin{equation} \bra{\psi} \left(\ket{\phi}+\ket{\xi}\right)=\braket{\psi }{ \phi} +\braket{\psi }{\xi} \end{equation}\]

Rovnako

\[\begin{equation} \left( \bra{\psi}+ \bra{\phi}\right)\ket{\xi}=\braket{\psi }{ \xi} +\braket{\phi }{\xi} \end{equation}\]

Z bilineárnosti skalárneho súčinu tiež vyplýva, že ak \(c\) je číslo, tak:

\[\begin{equation} c\braket{\psi}{\phi}=\bra{\psi}c\ket{\phi}=\braket{\psi}{\phi}c \end{equation}\]

Inak povedané, číslo môžeme výrazom zloženým zo zasebou zapísaných bra a ket ľubovoľne presúvať. Ale pozor: bra vektor k vektoru \(c\ket{\psi}\) je \(c^*\bra{\psi}\), kde \(^*\) značí komplexné združenie. Vyplýva to z požiadavky kososymetrickosti skalárneho súčinu [3]Kososymetrickosť znamená, že \(\braket{\psi }{ \phi}=\braket{\phi }{ \psi}^*\). Premyslite si to. .

Operátor

Operátor v kvantovej mechanike je mlynček. Na vstupe vezme stav zo stavového priestoru a do klobások natlačí iný (alebo aj rovnaký) stav.

\[\begin{equation} A\ket{\psi}=\ket{\phi} \end{equation}\]

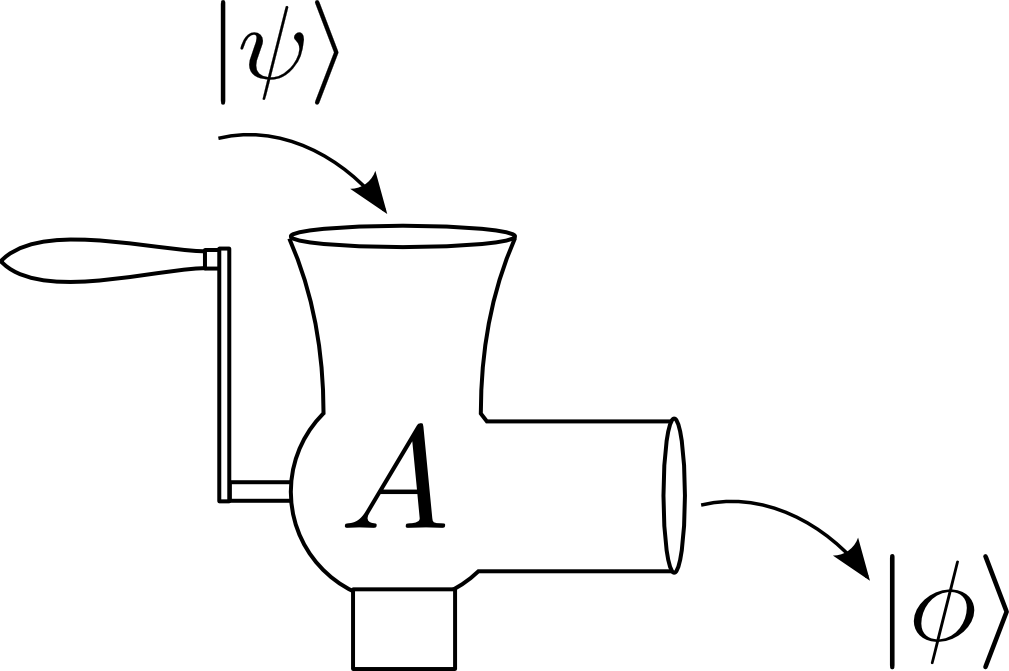
Operátory v kvantovej mechanike sú pritom vždy lineárne. Prečo? Aby zachovali charakteristickú črtu kvantovej mechaniky: princíp superpozície. Lineárne operátory majú pritom jednu skvelú vlastnosť: stačí zadefinovať, ako pôsobia na bázové vektory stavového priestoru. Predveďme si to na jednoduchom prípade dvojrozmerného stavového priestoru. Jeho bázové vektory budeme značiť \(\psi_1\) a \(\psi_2\). Majme všeobecný operátor \(A\). Zadefinujeme ho teda takto:

\[\begin{align} A \psi_1 = a \psi_1 + b \psi_2 \\ A \psi_2 = c \psi_1 + d \psi_2 \end{align}\]

Pričom \(a\),\(b\),\(c\),\(d\) sú komplexné čísla. (No jasne, veď to je obyčajný maticový zápis, poviete si. A máte pravdu.) Operátor \(A\) je teraz úplne zadefinovaný. Zapísať to pomocou bra a ket je jednoduché, ak máme k dispozícií dva riadky.

\[\begin{align} A \ket{\psi_1} = a \ket{\psi_1} + b \ket{\psi_2} \\ A \ket{\psi_2} = c \ket{\psi_1} + d \ket{\psi_2} \end{align}\]

Ako ale zraziť tento zápis do jedného riadku? Na to, aby to bolo možné, je potrebné, aby bola báza zložená z \(\ket{\psi_1}\) a \(\ket{\psi_2}\) ortonormálna (Oprava: Naozaj nutné je len aby bola úplná, ale v takom prípade by bol celý postup obludný. Ako by vyzeral bra-ket zápis pre nenormovanú, neortogonálnu, a nakoniec neortogonálnu a nenormovanú bázu už nechávam na zvedavých a masochystických čitaťeľov).

Takže:

\[\begin{align} \braket{\psi_1}{\psi_1} = \braket{\psi_2 }{ \psi_2 } =1 \\ \braket{\psi_1 }{ \psi_2} = 0 \end{align}\]

Teraz vám zvestujem, že výsledný zápis operátora \(A\) bude:

\[\begin{align} A &= \begin{aligned}[t] &a \ket{\psi_1}\bra{\psi_1} + b \ket{\psi_2}\bra{\psi_1}+\\ +&c \ket{\psi_1}\bra{\psi_2} + d \ket{\psi_2}\bra{\psi_2} \end{aligned} \end{align}\]

Zápis do dvoch riadkov je tu čisto estetický. Čo to teda vlastne znamená a prečo je to tak? Rozoberme si pôsobenie tohoto operátora na bázový stav \(\ket{\psi_1}\). Najprv obyčajne roznásobím:

\[\begin{align} A \ket{\psi_1} &= \begin{aligned}[t] &a \ket{\psi_1}\braket{\psi_1 }{ \psi_1} + b \ket{\psi_2}\braket{\psi_1 }{ \psi_1}+\\ +&c \ket{\psi_1}\braket{\psi_2}{\psi_1} + d \ket{\psi_2}\braket{\psi_2 }{ \psi_1} \end{aligned} \label{eq:a} \end{align}\]

Teraz vďaka ortonormálnosti bude \(\braket{\psi_2 }{ \psi_1}=0\) a \(\braket{\psi_1 }{ \psi_1}=1\). Takže prežije len prvý riadok, a teda:

\[\begin{equation} A \ket{\psi_1} = a \ket{\psi_1} + b \ket{\psi_2} \end{equation}\]

A je to. Obdobne pôsobí \(A\) aj na stav \(\psi_2\). Výraz \(\boldsymbol{c\ket{\psi_i}\bra{\psi_j}}\) teda pôsobí tak, že vylúpne všetky \(\boldsymbol{\ket{\psi_j}}\) a nahradí ich \(\boldsymbol{c \ket{\psi_i}}\).

Pekné, nie? Ako to bude pre všeobecný, viacrozmerný vektorový priestor (konečnorozmerný alebo spočítateľne nekonečnorozmerný)? Ľahko nahliadneme, že všeobecný operátor zapíšeme ako:

\[\begin{equation} A=\sum\limits_{i}{\sum\limits_{j}{c_{ij}{\ket{\psi_i}\bra{\psi_j}}}} \end{equation}\]

Tento zápis sa hodí hlavne vtedy, ak operátor (vo svojom maticovom zápise) má veľa nulových elementov. Napríklad jednotkový operátor (identita) bude [4] Toto si zapamätajte, tento výraz sa votrel snáď úplne všade. :

\[\begin{equation} I=\sum\limits_{i}{\ket{\psi_i}\bra{\psi_i}} \end{equation}\]

Príklad z praxe:

Ako zapísať zdvihový (nazývaný aj kreačný) operátor \(a^\dagger\) pre harmonický oscilátor? Jeho definícia je, že z ľubovoľného stavu \(\ket{n}\) urobí stav \(\ket{n+1}\) a prenásobí ho číslom \(\sqrt{n+1}\). Stavy \(\ket{n}\) pritom tvoria ortonormálnu bázu stavového priestoru. Priamo z definície:

\[\begin{equation} a^\dagger=\sum\limits_{n}\sqrt{n+1}\ket{n+1}\bra{n} \end{equation}\]

Je tiež celkom zrejmé ako zapísať operátor v prípade, že stavový priestor je nespočítatelne nekonečnorozmerný. Stačí sumy nahradiť integrálmi.

\[\begin{equation} A=\int\limits_{i}{\int\limits_{j}\ di \ dj \ {c(i,j){\ket{\psi_i}\bra{\psi_j}}}} \end{equation}\]

To by bolo všetko. Ak si chcete vyskúšať či tomu rozumiete, skúste pomocou bra-ket notácie zapísať tieto operátory:

• Hamiltonián harmonického oscilátora v báze \(\ket{n}\).
• Pauliho maticu \(\sigma_x= \begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix}\) v báze \(\ket{\uparrow}=\tvect{1}{0}\) a \(\ket{\downarrow}=\tvect{0}{1}\).