This is one of those wonderfully stupid questions that makes no sense at first glance, but you learn a lot when you think about it for a while. So what does this question even mean? Well, average mass is computed the same way every time: you sum masses of all things in a given category and then divide it by their count. For example average American weighs \(80 \mathrm{ kg}\) and average pineapple around \(2 \mathrm{ kg}\). The average mass of both pineapples and Americans together is approximately \(3,5 \mathrm{ kg}\) (there is simply much more pineapples than Americans). Ok, but we are not interested in some subsets like these, we want the average mass of EVERYTHING! Galaxies, planets, penguins, atoms, quarks! How much will that be?

We hit the first problem right at the beginning. If we, for example, include into our averaging a human, maybe we shouldn’t include individual human cells, since we have already included mass of every one of them. But if we define our question like that, the answer will tell us almost nothing. It would be quite trivial, namely that everything is only a part of the universe, and therefore only one thing exists- the universe. So let us instead define our question like this: imagine, that you are playing god [1] After all that is what scientist usually do, at least according to the movies. and from time to time you simply reach into the universe and take out some thing. It might be anything that somebody could sometime call “a thing”, regardless of wether it is a part of something bigger or not. You measure its mass, write it down on a paper and than return the thing into the universe. What interests us is the average mass written on your paper. What counts as “a thing” is of course still subjective, but with any luck, since we are attempting to do only an estimate, it won’t significantly influence the result. So let’s get to it. But wait! First you have to make an initial guess. Ready? Seriously, don’t continue without it! So, do you have a guess? Than let us move on.

What can still be considered a thing? The biggest possible thing is probably the universe (observable). It weighs \(m_{max}=10^{54} \mathrm{ kg}\) and it is one of a kind. Then after zooming a little we get to a lower scale and we find out that it consists of, let’s say, clusters of galaxies (Is it a thing, or not? We will leave that for later, as well as dark matter/energy). Then there are galaxies, then stars,…, molecules, atoms and finally elementary particles. We can stop for example at quarks, their mass is approximately \(m_{min}=10^{-30} \mathrm{ kg}\). Based on this, let us make a simple model of the universe: let it consist, on every scale, of only identical things. Of those, every one consists of \(N\) things on a smaller scale, which are therefore N times lighter, and so on down to the smallest particles as seen on the figure 1. We will call the \(N\) the scaling factor. If the \(N\) were for example 2, the universe would consist of two half-universes, every one of them of two quarter-universes and so on down to double quarks and finally quarks. It is obvious that \(N=2\) doesn’t make much sense, so it should probably be a bigger number, but let us leave that for later.

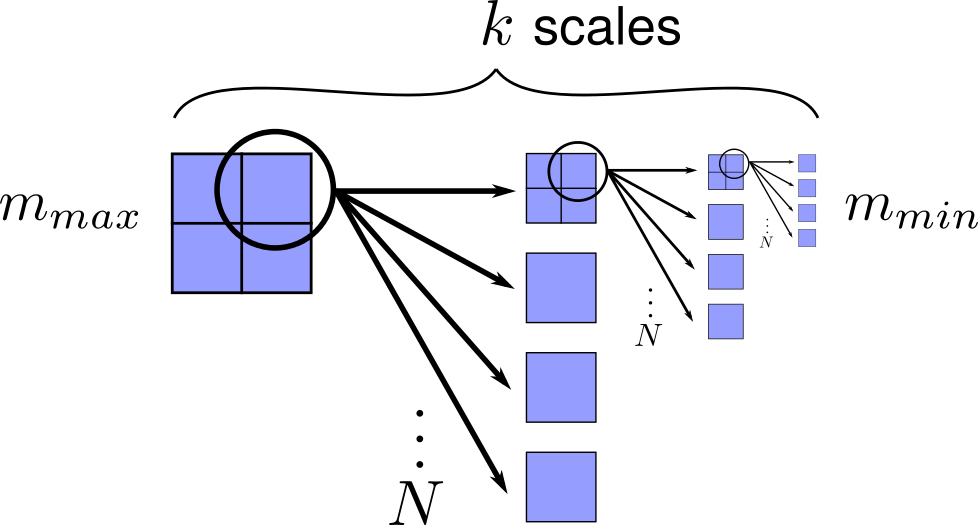
Fig. 1: Our model of the universe: everything consists of \(N\) smaller things. The universe is thus divided to \(k\) different scales. Therefore, at \(i\)-th scale there exists \(N^{i-1}\) objects.

With this model it is easy to write down the equation for average mass. Right from the definition (sum up masses of all things and divide it by their number):

\[\begin{equation}\begin{split}\widetilde{m} &= \frac{m_{max}+\frac{m_{max}}{N}N+\frac{m_{max}}{N^2}N^2+...+\frac{m_{max}}{N^{k-1}}N^{k-1}}{1+N+N^2+\dots+N^{k-1}} = \\ \\ &= \frac{m_{max}\cdot k}{1+N+N^2+\dots+N^{k-1}} \end{split}\end{equation}\]

Here \(k\) is the number of scales we divide our universe into (\(k=1+\log_N{\frac{m_{max}}{m_{min}}}\)). After a little bit of algebra [2] Sum of geometrical series \(1+N+N^2 \dots N^{k-1}=\frac{N^k-1}{N-1}\) and the fact that \(N^{k-1}=\frac{m_{max}}{m_{min}}\) and a few approximations [3] \(N^{k}-1 \approx N^{k} and \frac{N-1}{N} \approx 1\), we can get it into beautiful form:

\[\begin{equation}\widetilde{m} \approx k \cdot m_{min}\end{equation}\]

That is a surprisingly simple result for such a huge problem. We have found that the average mass of everything is simply a product of two variables: how many scales we divide the universe into and the mass of the smallest thing in the universe. Even better, it is always a very small number (since \(m_{min}\) is extremely small). The reason for this is simple: there is simply too many elementary particles and together they weigh, in the order of magnitude, almost as much as all of the universe. If you want to see it mathematically, then take a look at the denominator in the equation (1). That is a huge number, definitely much bigger than anything in the numerator. If you want something even deeper, than these two words should do it for you: exponential growth.

In what range can the average mass of everything even be? That depends on the scaling factor \(N\). The biggest possible \(N\) is \(N=10^{84}\), in which case the universe would have only two types of objects: the universe itself and quarks, nothing in between. Thus \(k=2\) and therefore the average mass will be of the order of the mass of elementary particles. The opposite extreme is a very small scaling factor. The smallest reasonable value is probably \(N=2\) (every thing consists of two smaller things). But even than, the universe would be divided only to a meager \(k=280\) scales and the average mass of everything would rise only by two orders of magnitude.

Well, you might say, but our initial assumptions were not completely kosher. In reality, some things consist of objects that are multiple scales lower than them and scales are thus “skipped”. For example stars consist directly of atomic nuclei and electrons. Therefore, we jump from the scale of stars( the Sun weighs approximately \(10^{30} \mathrm{ kg}\)) right to the scale of elementary particles (\(10^{-27} \mathrm{ kg}\) and less), thus completely avoiding the scale of human dimensions. Furthermore, the scaling factor is not constant throughout the different scales. And what about the dark matter or energy? And the bounding energy, which contributes to the mass of atomic nuclei (and other things) according to the \(E=mc^2\)?

Since this is not a scientific article but just an answer to the silly (but good!) question, I will inconspicuously skip those objections. However, I will provide a few arguments why I think they would not matter anyway. It is important to realize, that when it comes to averages, the most influence is not on the side of the things with the biggest mass, but on the side of those with the bigest numbers. Lets take, for example, the dark energy. It comprises two thirds of the universe, but still it is only one object [4] It is possible that one day our children will learn at schools that it consists of something, but for now it is usually considered as one thing. . On the other hand, there is \(10^{84}\) of elementary particles and together, they weigh in an order of magnitude almost as much as the dark energy. They will therefore completely dominate the average mass. For something to significantly influence the result, there would have to be a lot of it, and therefore it would have to be light, so it would not matter anyway. Another problem was the skipping of scales. The equation (1) can be modified to account for that by simple change:

\[\begin{equation}\begin{split}\widetilde{m}&=\frac{m_{max}+f_1 m_{max}+f_2 m_{max}+ \dots +f_{k-1}m_{max}}{1+N+N^2+\dots+N^{k-1}}= \\ \\ &=\frac{\widetilde{f}\cdot m_{max}\cdot k}{1+N+N^2+\dots+N^{k-1}}\end{split}\end{equation}\]

where \(f_i\) is the ratio of overall mass of all things on i-th scale to the mass of the universe. This equation can be however simplified with the use of average value of this parameter \(\widetilde{f}\), which is by definition smaller than 1, and the rest of the equation is the same as in equation (1). Therefore the skipping of the scales can only lower the result even more.

We came to a serious answer: the average mass of everything is somewhere at the level of elementary particles (give or take two orders of magnitude). What to take from that? Something about the exponential growth: it is the reason why there is so many, many,…, many elementary particles. Another thing to remember is something about the averages: they erase anything that is an exception. And when it comes to the universe, anything heavier than an elementary particle IS an exception.